This post title is quite a mouthful. I haven’t written in a while, so I have quite a bit to dump out. I’ll just throw some seemingly unrelated ideas, and see what happens.

- Tenenbaum’s Blessing of Abstraction

[The] abstract layer of knowledge can serve a role as inductive bias even when the abstract knowledge itself must be learned. Learning a theory of causality is as good (from the perspective of causal model learning) as having an innate theory of causality.

Main takeaway: In the framework of hierarchical Bayesian modelling, learning the higher, more abstract levels at the same time of learning the lower levels seems to work just fine. It is even helpful, and Tenenbaum calls this the Blessing of abstraction.

- Hinton’s greedy layer-wise pretraining

You train layers of a RBM one at a time. Then freeze. Then take the output of the last layer, and treat as input to train the next layer. Each time you do that, you improve on a variational lower bound (whatever that means, it feels good to say it though)

Note: We no longer bother with this (explanation by Karpathy why)

- Tenenbaum causal grammar proposal 1 (2 is here)

At page 22 of the first proposal, we have this cutie:

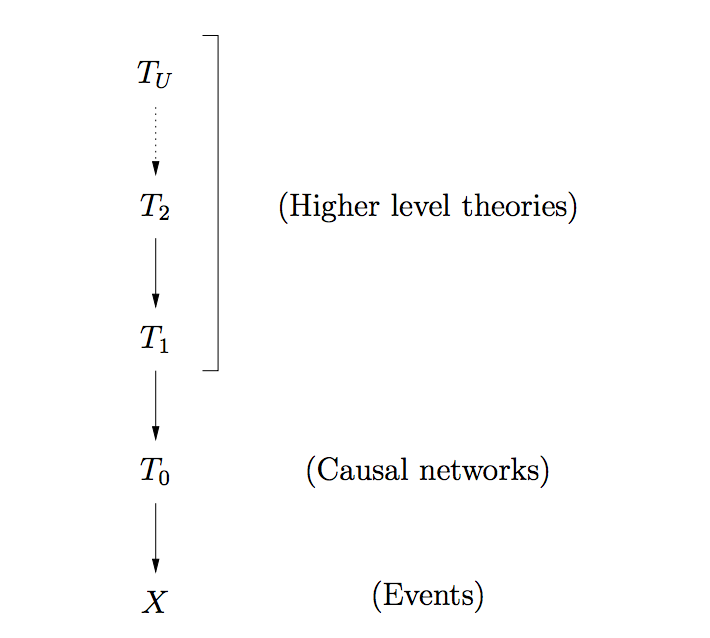
Figure 4. A hierarchical probabilistic model corresponding to the hierarchy of abstraction in causal theories shown in Figure 3. Theories at each level of abstraction define a prior probability distribution over candidate theories at the next level down, bottoming out in the observed data X. Bayesian inferences about theories at each level combine information from the observed data, propagated upwards by successful lower-level theories, with top-down constraints from higher-level theories (and ultimately perhaps some universal conceptual skeleton for all theories, Tu ).

Kind of reminds the p(v|h,W) thing just above

- Tenenbaum thick arrows

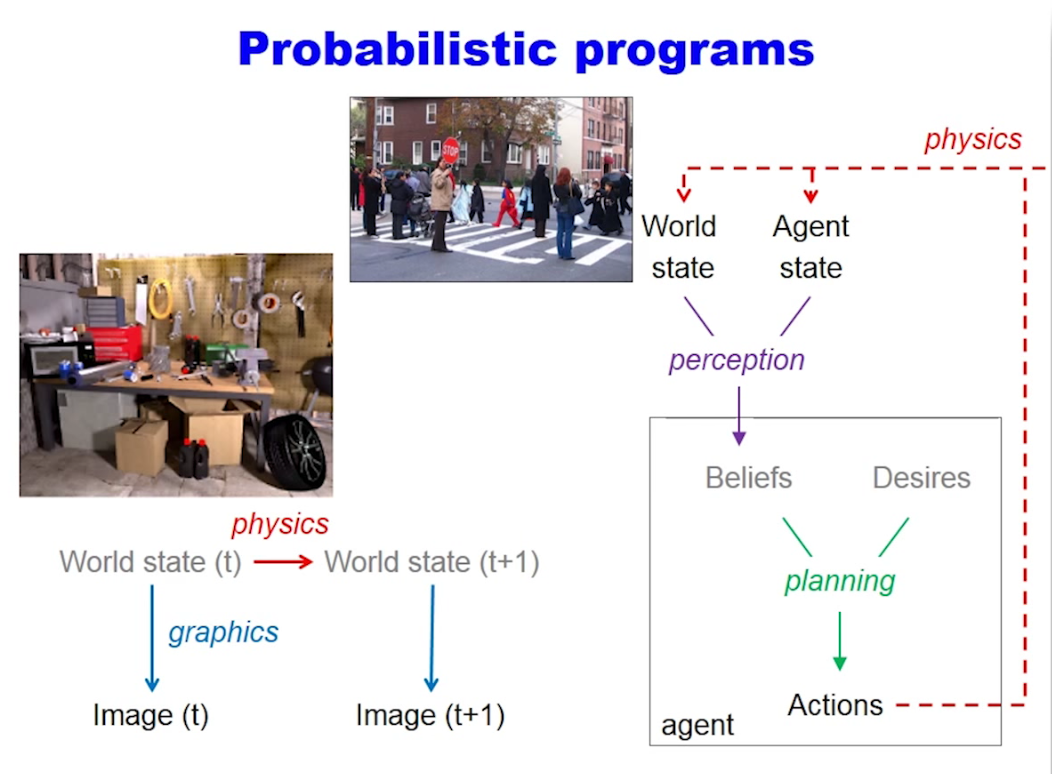
Look at those arrows! So slick, so simple. Surely, nothing complicated is happening there. Physics? What's that?

Not related to the previous points. Just a general criticism about bayes nets / graphical models.

- Limitations of linear combinations of features

at page 25:

A more principled approach, from the perspective of ensuring a more robust compact feature representation, can be conceived by reconsidering the disentangling of features through the lens of its generative equivalent – feature composition. Since many unsupervised learning algorithms have a generative interpretation (or a way to reconstruct inputs from their high-level representation), the generative perspective can provide insight into how to think about disentangling factors. The majority of the models currently used to construct invariant features have the interpretation that their low-level features linearly combine to construct the data. This is a fairly rudimentary form of feature composition with significant limitations. For example, it is not possible to linearly combine a feature with a generic transformation (such as translation) to generate a transformed version of the feature. Nor can we even consider a generic color feature being linearly combined with a gray-scale stimulus pattern to generate a colored pattern. It would seem that if we are to take the notion of disentangling seriously we require a richer interaction of features than that offered by simple linear combinations.

Totally related to the thick arrows idea.

Discussion

On the mechanics of the Blessing of abstraction

To take the first related two points, it’s interesting to note that in the Hinton setting, we are creating the layers bottom-up, while in the Tenenbaum setting, we are learning all the levels at the same time. This may be an apple to orange comparison, because Hinton works with RBMs, and Tenenbaum in some abstract bayesian probabilistic setting (that I don’t fully understand). But still, this idea of learning all the levels at the same time, and having the higher ones guide you with the lower ones (aka blessing of abstraction) is fascinating to me. Speculation: Would it be possible to have this effect also work in the RBM setting? Or in the more classical convnet-with-backprop-and-SGD setting?

On the seemingly too naive linear combinations (but still dang effective, possible explanation why)

Just combining features with linear combinations (and a few relus here and there) seem to work very well. But still, linear combinations feel too simple. Just to hammer this point home:

This [linear composition] is a fairly rudimentary form of feature composition with significant limitations. For example, it is not possible to linearly combine a feature with a generic transformation (such as translation) to generate a transformed version of the feature.

We need to be able to compose stuff.

Speculation: Go back a few slides in the Hinton video to the italian slide, then make those arrows thick! That’s it. Implementation details are left as an exercise for the reader.

Well, those details actually matter. So let’s see what would happen. Being thick would mean that they are not just number-passing or simple linear combinations, but whole function or even programs. How do we pick those functions? I don’t know.

Another problem is that in the diagram, those arrow run in both directions: forward (recognition / bottom-up) and backward (generation / causal / physics engine direction). So how do we make our function runnable in both directions? For inspiration:

• This is a way to run a convnet backwards
• This is a way to invert a graphics program
• This is a way to inverse a generative blackbox
• And yet other ways

But here we are interested in inverting what is most likely a much simpler function. Or even inducing this function from the very beginning so that it can run both ways.

I may come back to this thickening problem later (hoping the reader took the exercise)

Other less retated ideas, but worthy of mention because they are amazing:

• Bayesian Program Learning

This can be viewed as a successful application of the thickening of arrows that we failed just above. Little pieces of programs that compose, induced in a bayesian way. Not bad. Looks pretty specific to handwritten digits though, would be cool to see ways of generalizing this approach.

• The discovery of structural form

Another unrelated note…

From Josh Tenenbaum: Engineering & reverse-engineering human common sense

From The Next Generation of Neural Networks

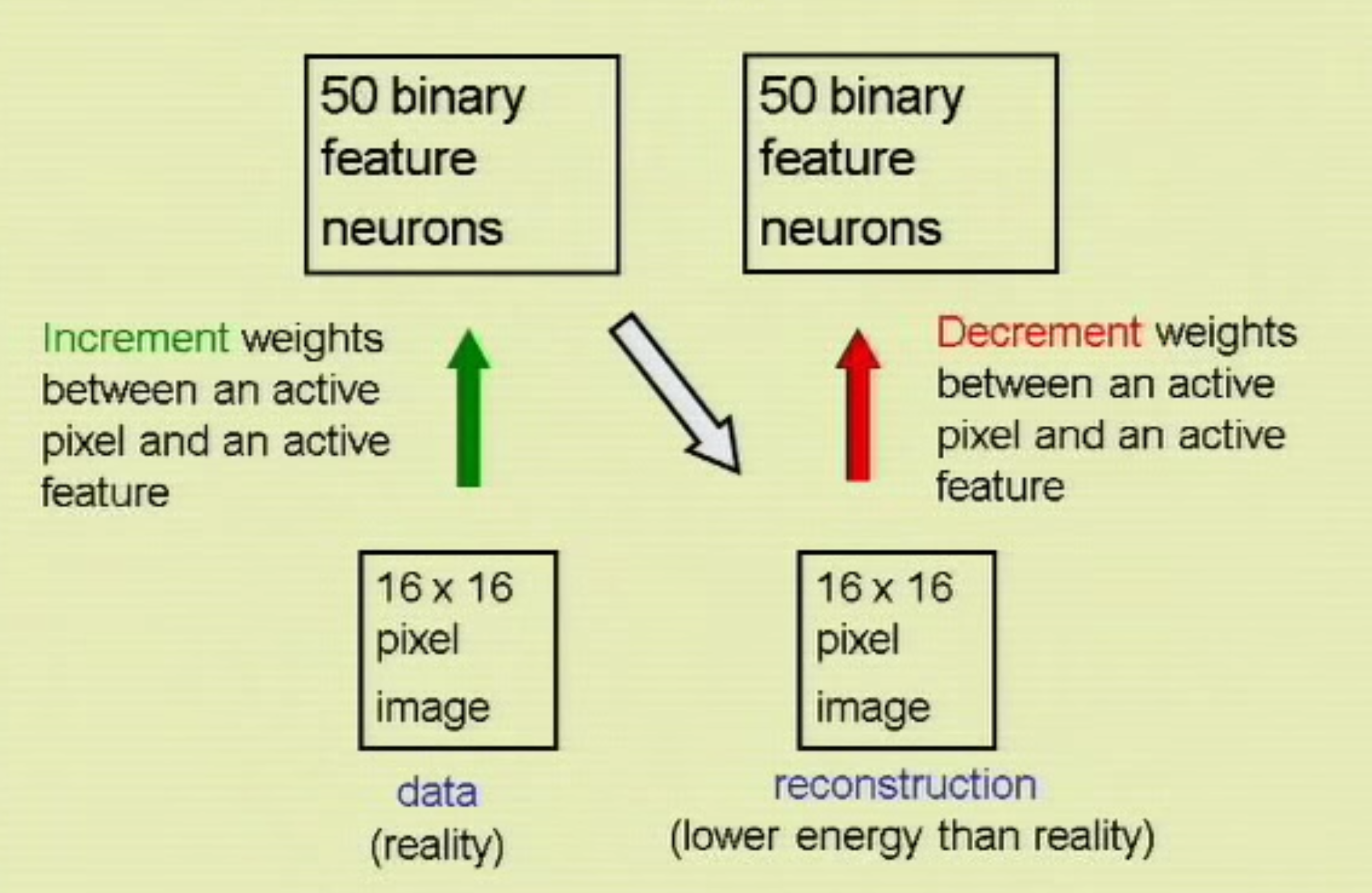
Now if you squint hard enough…

After some thought, the up/down direction is about the same, but the left/right direction is time in the Tenenbaum diagram, while it’s a “step in a gibbs sampling process” in the Hinton diagram. Meaning that (in the 2nd diagram) there is no notion of time, just the notion that we are trying to see what the networks belives in, based on the data.

So the analogy does not quite hold.