Josh Tenenbaum and Noah Goodman have this concept that the arrows in a bayes net (or graphical* model) need to be infinitely thick, and that’s a big motivation behind probabilistic programs.

*graphical model in the sense of “graph” here. Not “graphics”.

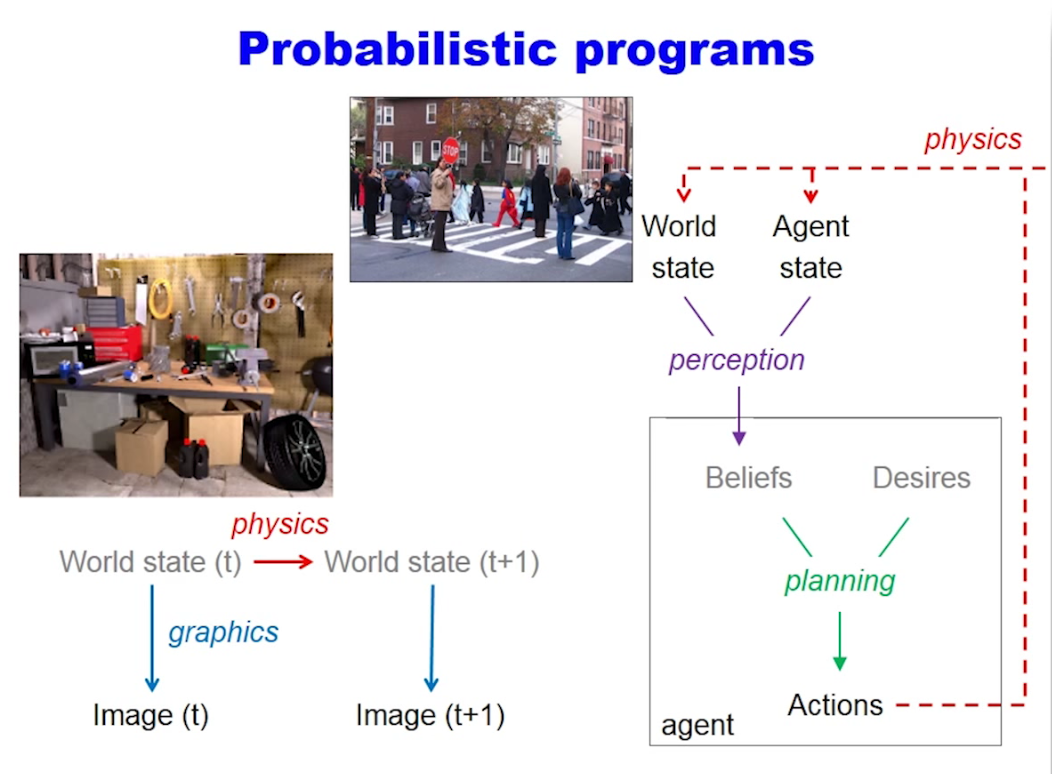
Quoting Josh Tenenbaum:

But the basic idea [about probabilistic programs] is to say: “define these world models”. You could look at this and you could say: “well these look like directed graphs, why is that different from bayes nets”, and is some sense that might be right. If you know the directed graph formulation of a hidden markov model, the picture I’m showing down here kind of looks like that. But the key is that if you were to represent this as a traditional bayes net or graphical model, you’d have nodes and arrows that are infinitely thick. The world state isn’t just a fixed finite-dimensional random variable, but it’s something like a whole CAD description of a scene (we don’t really know how to describe this yet) but it’s a description of a whole bunch of physical objects in a three dimensional representation, with their physical properties like masses and stiffnesses and so on. And this arrow isn’t just a transition matrix in an HMM, but rather it’s a physics simulator. So we think if you really want to capture intuitive physics, vision, intuitive psychology, you need these “thick arrows” that we really can only capture with programs, the same way in many other areas of science where that’s the main way we capture our knowledge.


Bonus: related