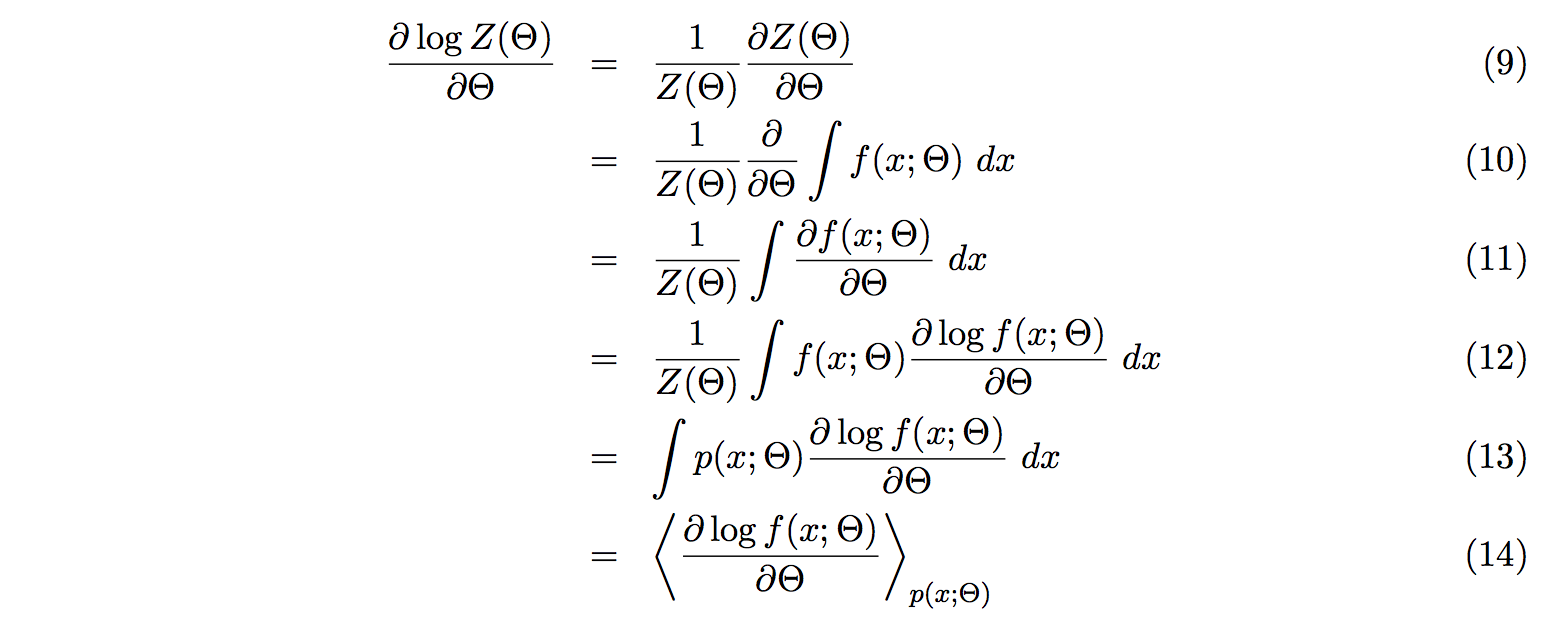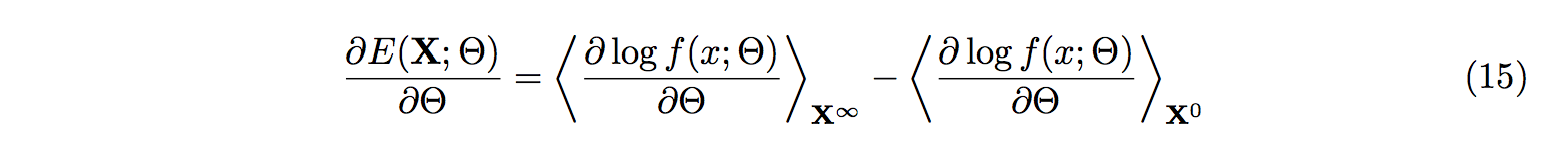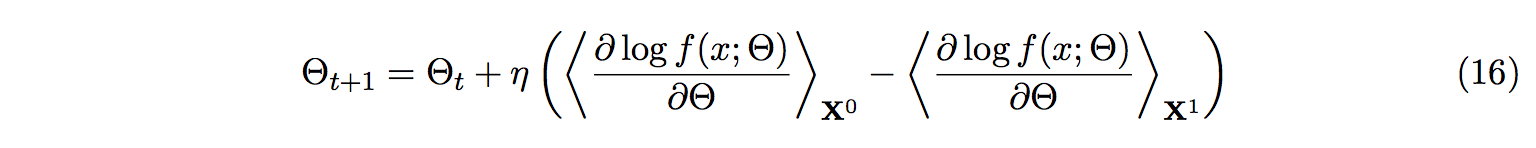For a long time, I did not get how contrastive divergence (CD) works. I was stumped by the bracket notation, and by “maximizing the log probability of the data”.

This made everything clearer: http://www.robots.ox.ac.uk/~ojw/files/NotesOnCD.pdf.

Local copy here (in case website is down)

The only math needed is integrals, partial derivatives, sum, products, and the derivative of the log of an arbitrary function. (log u)' = u' / u.

Just so the math fits on one screen, I’ll put the equations below.

x is a data point. f(x; Θ) is our function. Θ is a vector of model parameters.

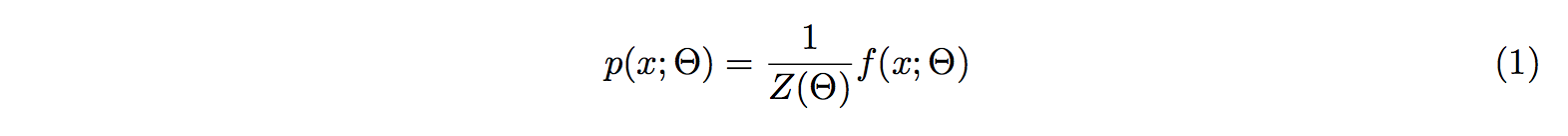
Z(Θ) is the partition function.

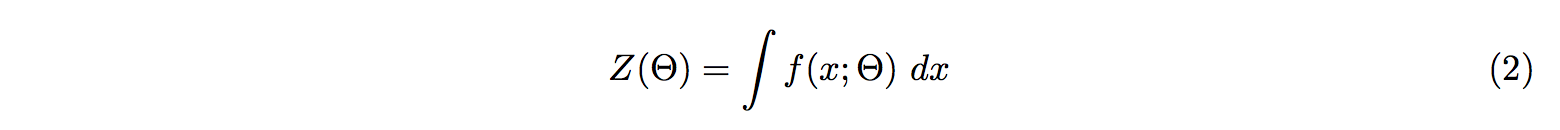
We learn our model parameters, Θ, by maximizing the probability of a training set of data, X = x1,..,K, given as

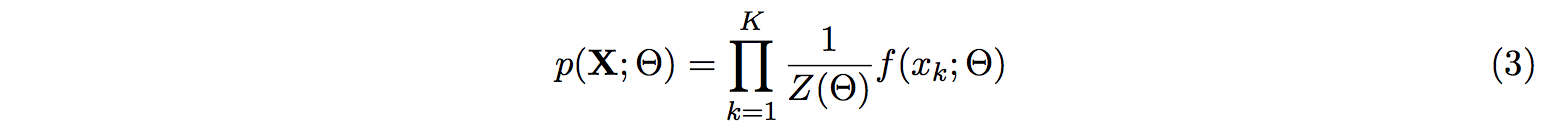
Which is the same as minimizing the energy E(X; Θ)


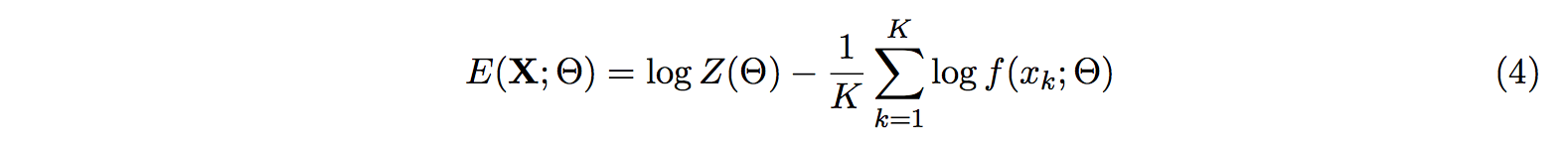
We derive the energy with respect to the model parameters, Θ

Quick explanation for (7): for first bit d log Z(Θ), we just put the d/dΘ on top of it. For the second bit, we put the d/dΘ inside the sum.

Quick explanation for (8): The sum is rewritten with the bracket notation.


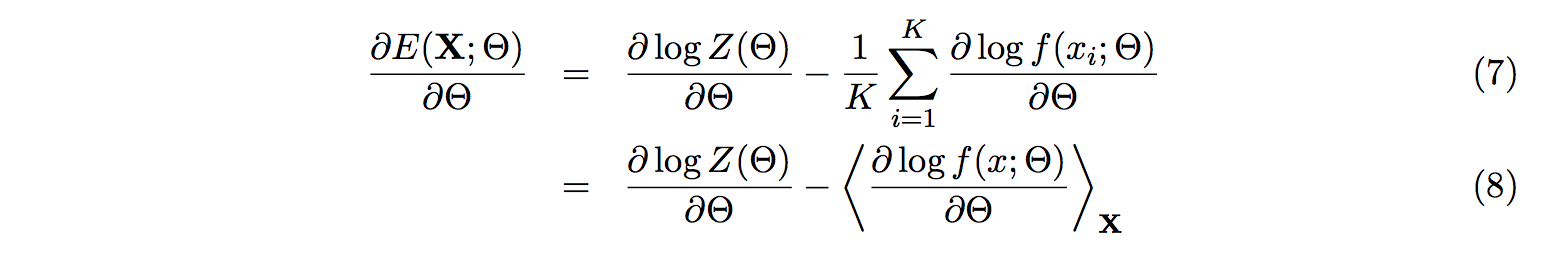
Here we calculate the first bit of the energy derivative of (7)

(9): We use (log u)' = u' / u

(9 -> 10): We use the definition of Z. See (2)

(10-> 11): Easy

(11 -> 12): We use (log u)' = u' / u again.

(12 -> 13): We use the definition of p. See (1)